Merge sort

Pokročilé řadicí algoritmy

SSŠVT

Merge sort

Obsah

1. Princip
2. Algoritmus
   1. Operace Merge
   2. Vlastní Merge sort
   3. Naznačení implementace
3. Ilustrace
4. Animace
5. Příklad
6. Odkaz

Princip

Merge sort je případem strategie rozděl a panuj (divide and conquer). Nejprve vstupní nesetříděnou kolekci porovnatelných prvků rozdělí na menší kolekce. Potom každou z nich setřídí a nakonec je spojí operací Merge na výslednou setříděnou kolekci.

Dělení kolekcí lze rekurzivně opakovat až se dostaneme na malé (např. jednoprvkové) kolekce, jejichž setřídění je triviální.

Algoritmus

Operace Merge

Merge sort používá spojování dvou již setříděných kolekcí do jedné větší, taktéž setříděné. Této operaci říkáme Merge.

Popis operace Merge:

Mějme tedy 2 menší setříděné kolekce, označme je A a B, a jednu (na začátku prázdnou) kolekci, kde bude výsledek, tj. všechny prvky z obou kolekcí A i B, již ve správném pořadí. Označme výslednou kolekci Z. Třídíme od nejmenšího prvku po největší.

1. Vezmeme první prvek z kolekce A, označme ho a, a první prvek z kolekce B, označme ho b.
2. Prvek a je momentálně nejmenší prvek z kolekce A, zatímco b je nejmenší prvek z kolekce B.
3. Je-li a menší nebo rovno než b, odebereme prvek a z kolekce A a přidáme ho na konec kolekce Z.
4. Je-li a větší než b, odebereme prvek b z kolekce B a přidáme ho na konec kolekce Z.
5. (Druhý z prvků zatím ponecháme v jeho původní kolekci. Tj. např. pokud jsme odebrali b z kolekce B, protože b bylo menší než a, pak prvek a prozatím zůstává na prvním místě v kolekci A.)
6. Postup v cyklu opakujeme.
7. Pokud je jedna ze vstupních kolekcí A nebo B již prázdná, dobereme postupně prvky z té druhé kolekce. (Nemusíme je s ničím porovnávat, jsou setříděné.)
8. Jakmile jsou obě vstupní kolekce prázdné, máme v Z celou výstupní setříděnou kolekci.

Vlastní Merge sort

Než začneme s "merge-ováním", musíme nejprve kolekci, kterou chceme setřídit, rozdělit na triviální jednoprvkové kolekce. Pokud má celá vstupní kolekce n prvků, pak vytvoříme na začátku n jednoprvkových kolekcí. V každé bude jeden prvek z té kolekce, kterou třídíme.

Jednoprvkové kolekce jsou již "setříděné". Rozdělíme si tyto kolekce po dvojicích a na každou dvojici aplikujeme operaci Merge.

• Pokud je n sudé, vznikne nám n/2 dvouprvkových setříděných kolekcí.
• Je-li n liché, dostaneme (n-1)/2 dvouprvkových setříděných kolekcí a jednu jednoprvkovou, kterou zatím nemáme s čím spojit.

Vzniklé dvouprvkové kolekce (a případně jednu jednoprvkovou) opět rozdělíme po dvojicích a aplikujeme operaci Merge. Tím nám vzniknou čtyř-, případně tří-prvkové kolekce. Ty opět mezi sebou pospojujeme pomocí Merge atd.

Poznámka: Pokud použijeme rekurzi, je dobré provést rozdělení výchozí kolekce na jednoprvkové kolekce např. takto:

• Pokud je v kolekci, kterou dělíme, sudý počet prvků, rozdělíme ji na dvě stejné části, každá bude mít polovinu prvků.
• Pokud je v kolekci lichý počet prvků, rozdělíme ji na dvě téměř stejné části, v první bude o jeden prvek více než ve druhé.
• Jednoprvkové kolekce dále nedělíme.
• Postup rekurzivně opakujeme, až máme samé jednoprvkové části.

Nazvěme výše popsanou operaci dělení kolekce na dvě jako Divide.

Naznačení implementace

V pseudo-kódu podobném C# nyní popíšeme celý rekurzivní postup:

• Máme hlavní metodu Sort, která má jeden vstupní parametr (nesetříděná kolekce) a jeden výstupní parametr (kolekce se stejnými prvky, jaké má vstupní kolekce, ale nyní již v setříděném stavu).
• Máme metodu Divide, která má jeden vstupní parametr (nesetříděná kolekce, kterou dělíme napůl) a dva výstupní parametry, tj. dvě části původní kolekce.
• Prvky ve výstupních kolekcích metody Divide kopírují pořadí prvků ve vstupní kolekci. Tato metoda tedy skutečně pouze "rozsekne" původní kolekci na půlky (nebo skoro stejně velké části).
• Dále máme metodu Merge, která má dva vstupní parametry (dvě setříděné kolekce) a jeden výstupní parametr (spojená setříděná kolekce).
• K tomu máme pomocnou metodu Subrange, která vrátí část kolekce jako novou kolekci podle zadaných parametrů (od indexu, do indexu).

// U... unsorted
// S... sorted

void Sort(in List U, out List S)
{
    // Trivial one-element collection is sorted by definition.
    if (U.Count == 1)
    {
        S = Subrange(U, 0, 0);
        return;
    }

    // Bigger collections must be divided first.
    List UA;
    List UB;
    Divide(in U, out UA, out UB);

    // Sort either collection.
    List SA;
    List SB;
    Sort(in UA, out SA);
    Sort(in UB, out SB);

    // Merge the sorted collections together into one (also sorted).
    Merge(in SA, in SB, out S);

    // Done.
}
        

void Divide(in List U, out List UA, out List UB)
{
    // Assume U has AT LEAST two elements.
    int divisionPoint = (U.Count + 1) / 2;

    // Get 1st half.
    UA = Subrange(U, 0, divisionPoint - 1);

    // Get 2nd half.
    // 2nd half shall have the same number of elements as 1st half
    // or it might be by one element less than 1st half.
    UB = Subrange(U, divisionPoint, U.Count - 1);
}
        

void Merge(in List SA, in List SB, out List S)
{
    S = new List();
    // Implementation explained above.
}
        

List Subrange(in List L, int fromIndex, int toIndex)
{
    List Sub = new List();
    // Implementation obvious.
    return Sub;
}
        

Poznámka: Metoda Subrange se chová jako funkce (vrací hodnotu). Ostatní metody (Sort, Divide a Merge) jsou procedury.

Máme-li vstupní nesetříděnou kolekci X a chceme-li získat její setříděnou variantu Y, pak stačí: Sort(in X, out Y);

Ilustrace

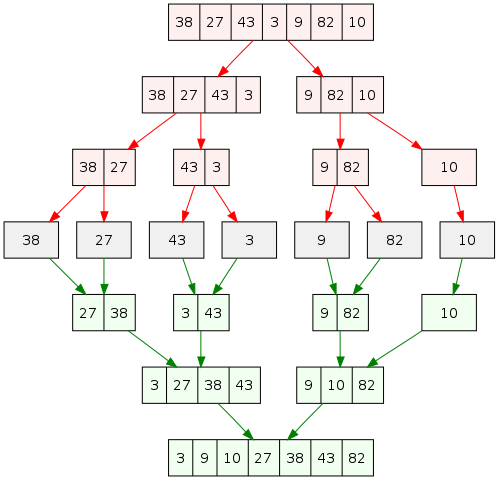
Třídíme kolekci čísel: 38, 27, 43, 3, 9, 82, 10

Animace

Zde třídíme kolekci čísel: 6, 5, 3, 1, 8, 7, 2, 4

Příklad

Chceme např. setřídit takovouto kolekci čísel: 10, -5, 2, 0, 12, 1

Odkaz

Více informací: https://en.wikipedia.org/wiki/Merge_sort