Quicksort

Pokročilé řadicí algoritmy

SSŠVT

Quicksort

Princip

Zvolíme některý prvek z kolekce (pokud možno s mediánovou hodnotou), nazveme ho pivot, a rozdělíme kolekci na dvě části tak, že v levé části budou prvky menší než pivot a v pravé části prvky větší než pivot. Pivot dáme mezi ně. (Prvky stejné jako pivot, tj. které jsou rovné pivotu, dáme např. do levé části.) Pokud výsledek takovéhoto "dělení" opět uložíme do nějaké kolekce, tak v ní máme nyní tři části:

  1. Nalevo: Nesetříděná část, v níž jsou ale všechny prvky menší nebo rovné pivotu.
  2. Uprostřed: Jednoprvková část - námi zvolený pivot.
  3. Napravo: Nesetříděná část, v níž jsou zase všechny prvky větší než pivot.

Potom vezmeme každou z částí (napřed levou, pak pravou) a rekurzivně postup opakujeme. Tj. v dané části vybereme opět její pivot a rozdělíme ji (analogicky jako při prvním dělení) na dvě podčásti, v jedné budou prvky menší než tento pivot, ve druhé budou prvky větší než tento pivot.

Pokud má některá část už jen jeden prvek, považujeme ji za "setříděnou". Postup opakujeme, dokud nezískáme samé jednoprvkové části.

Pokud jsme toto pivotové "dělení" provedli tzv. in-place, tj. ve zdrojové kolekci, tak po provedení všech dělení až na jednoprvkové části je kolekce setříděna.

Poznámka: Jako pivot můžeme v každé části, na kterou chceme aplikovat "dělení", vybrat např. její poslední prvek (viz ilustrace).

Ilustrace

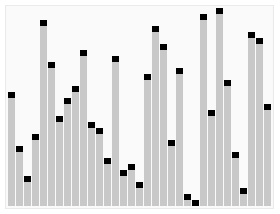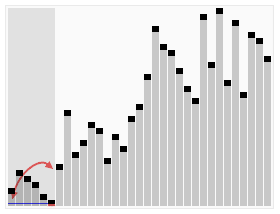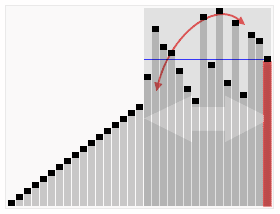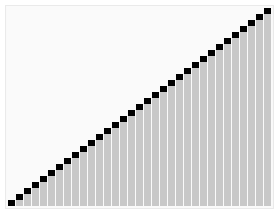
Quicksort Example

Příklad

Chceme např. setřídit takovouto kolekci čísel: 10, 0, 14, 2, -5, 12, 1

First level - pivot: 1
100142-5121
100142-5121
100142-5121
0-510142121
0-511014212
Second level LEFT part - pivot: -5
0-511014212
0-511014212
0-511014212
-5011014212
Second level RIGHT part - pivot: 12
-5011014212
-5011014212
-5011014212
-5011021412
-5011021214
Third level - left half of the RIGHT PART - pivot: 2
-5011021214
-5011021214
-5011021214
-5012101214
DONE

Odkaz

Více informací: https://en.wikipedia.org/wiki/Quicksort